Cut-Pursuit Algorithm for Regularizing Nonsmooth Functionals with Graph Total Variation

Loïc Landrieu's cut-pursuit algorithm is a very efficient working-set approach for minimizing the sum of a differentiable functional with a graph total variation regularization (and also nonconvex variations thereof).
As many applications involve other nondifferentiable terms, we extended it to the minimization of functionals, structured over a weighted graph G = (V, E, w), of the form

    F: x ↦ f(x) + ∑v ∈ V gv(xv) + ∑(u,v) ∈ E w(u,v) ║xu − xv║ ,

where x ∈ ℍV for some base vector space ℍ, f is differentiable, and for all v ∈ V, gv: ℝ → ]−∞,+∞] admits directional derivatives on every points of its domain and every directions.
The cut-pursuit algorithm seeks partitions V = (U1,...,U|V|) of the set of vertices V, constituting the constant connected components of the solution, by successively solving the corresponding problem, structured over the reduced graph G = (V, E), that is

  arg minξ ∈ ℍV    F(x) , such that ∀ U ∈ V, ∀ u ∈ U, xu = ξU ,

and then refining the partition, by using the directional derivatives and well-thought graph cuts.
A key requirement is thus the ability to solve the reduced problem, which often have the exact same structure as the original one, but with much less vertices |V| ≪ |V|. If the solution of the original problem has only few constant connected components in comparison to the number of vertices, the cut-pursuit strategy can speed-up minimization by several orders of magnitude.
Indeed, our first numerical experiments show tremendous improvement over state-of-the-art proximal splitting methods:
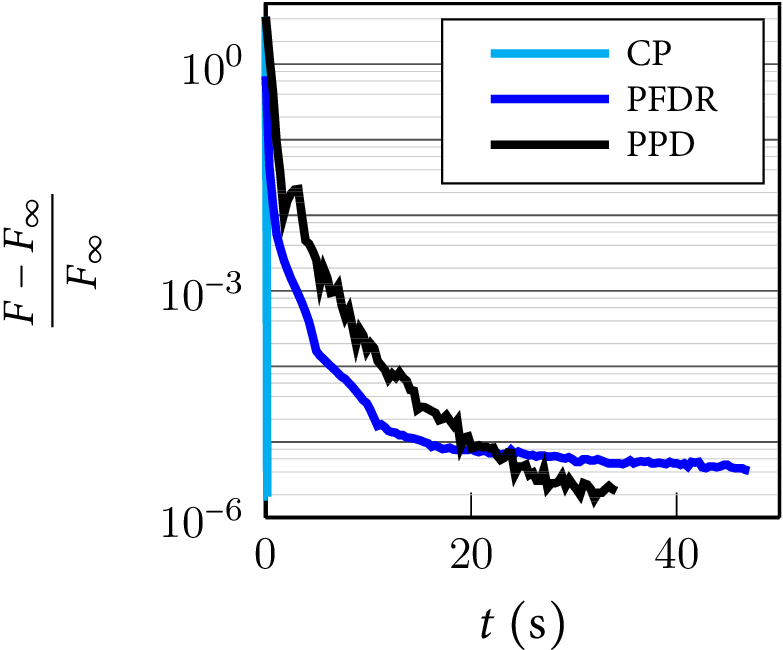
medium-scale setting of brain source identification for electroencephalography (|V| = 19 626, |E| = 29 439), using fused LASSO

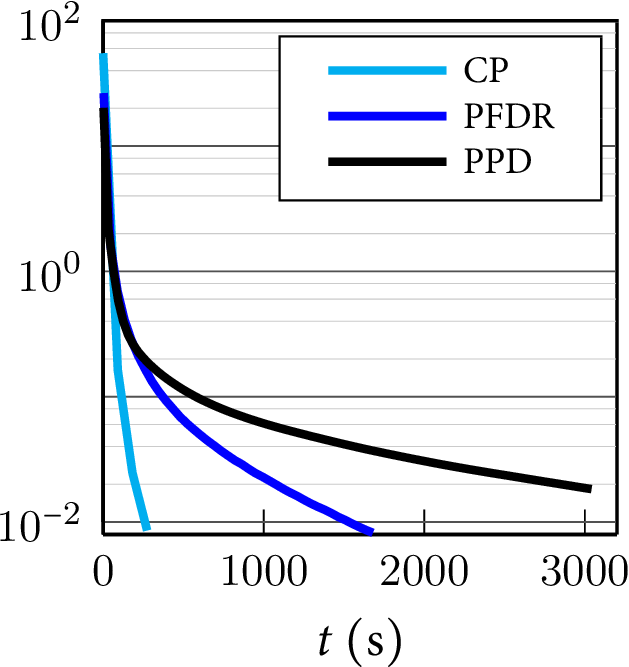
large-scale multidimensional setting of semantic labeling of 3D point cloud (|V| = 3 000 111, |E| = 17 206 938), using simplex-constraint convex relaxation

This has been published in the 35th International conference on machine learning: paper; reference as BibTeX format.
More details can be found in our preprint.
Optimized C++ implementations, interfaced with GNU Octave or Matlab and Python, can be found at the dedicated GitLab repository.
This is a joint work with Loïc Landrieu.


Back To Home